Ας υποθέσουμε ότι σας δίνεται ένας χάρτης, ο οποίος χωρίζεται σε διαφορετικές περιοχές όπως η επόμενη εικόνα.
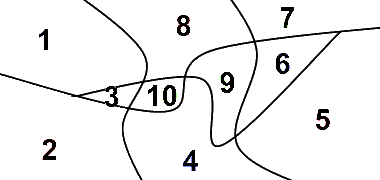
Στόχος μας είναι ο χρωματισμός των περιοχών του χάρτη με 4 διαφορετικά χρώματα έτσι ώστε γειτονικές περιοχές να έχουν διαφορετικό χρωματισμό. Έτσι, ο παραπάνω χάρτης πρέπει να έχει, για παράδειγμα, την επόμενη μορφή.
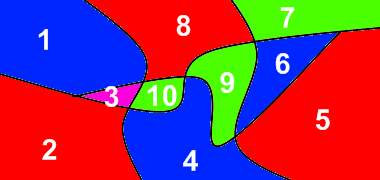
Να γίνει αλγόριθμος που να εκτελεί την παραπάνω εργασία. Συγκεκριμένα θα δέχεται ως δεδομένα έναν πίνακα Χ[4] με τα τέσσερα χρώματα που θέλουμε να χρωματίσουμε τον χάρτη, κι έναν πίνακα Γ ΝxN, με λογικές τιμές οι οποίες θα δείχνουν αν δυο περιοχές του χάρτη είναι γειτονικές. Δηλαδή, όταν Γ[i,j] είναι αληθής τότε η περιοχή i με την περιοχή j είναι γειτονικές. Όταν δεν είναι τότε είναι ψευδής. Σε περίπτωση αποτυχίας χρωματισμού με τέσσερα μόνο χρώματα να τυπώνεται κατατοπιστικό μήνυμα.
Αλγόριθμος Χρωματισμός_Χάρτη
Δεδομένα // Χ, Γ, N //
!Χ είναι ένας πίνακας 4 θέσεων στον οποίο καταχωρούνται τα χρώματα π.χ. Χ[1] <- ‘Κόκκινο’ κ.ο.κ
!Γ είναι ένας δισδιάστατος πίνακας NxN στον οποίο καταχωρούνται λογικές τιμές σχετικά με το αν δύο περιοχές είναι γειτονικές.
!N είναι ο αριθμός των περιοχών
!ΧΠ είναι ο πίνακας που καταχωρεί το χρώμα κάθε περιοχής.
!Αρχικά καμία περιοχή δεν είναι χρωματισμένη.
Για i από 1 μέχρι Ν
ΧΠ[i] <- 0
Τέλος_επανάληψης
Για i από 1 μέχρι Ν
Για k από 1 μέχρι 4
!Υποψήφιο χρώμα για την περιοχή
ΥΧΠ[k] <- ΑΛΗΘΗΣ
Τέλος_επανάληψης
Για j από 1 μέχρι Ν
Αν (i <> j) ΚΑΙ Γ[i, j] = ΑΛΗΘΗΣ ΚΑΙ ΧΠ[j] <> 0 τότε
ΥΧΠ[ΧΠ[j]] <- ΨΕΥΔΗΣ
Τέλος_αν
Τέλος_επανάληψης
βρέθηκε <- ΨΕΥΔΗΣ
k <- 1
Όσο k <= 4 KAI βρέθηκε = ΨΕΥΔΗΣ επανάλαβε
Αν ΥΧΠ[k] = ΑΛΗΘΗΣ τότε
ΧΠ[i] <- k
βρέθηκε <- ΑΛΗΘΗΣ
Εμφάνισε "Στην περιοχή ", i, "τοποθετήθηκε το χρώμα ", Χ[k]
Αλλιώς
k <- k + 1
Τέλος_αν
Τέλος_επανάληψης
Αν (ΟΧΙ(βρέθηκε)) τότε
Εμφάνισε "Αδυναμία καταχώρησης χρώματος στην περιοχή ", i
Τέλος_αν
Τέλος_επανάληψης
Τέλος Χρωματισμός_Χάρτη
